2)<x>=3となる2桁の整数をすべて答えよ。 例3.生徒5人のテスト点数について、2人ずつ得点を合計した。 1か381であるが、との7桁の数が7で割り切れるかどうかを調べると、前者は7で割り切れないから、答えは、と決まる。素数と暗号について 中川仁 平成19年7月10, 24日 rsa暗号についてお話しします.電卓またはノートパソコン持参のこと. 目次 1 エラトステネスの篩 1 2 オイラーの定理 3 3 gm におけるべきの計算 4 4 ユークリッドの互除法とその応用 4 5 rsa暗号 5 1この関数は、15桁以内の任意の(負でない)整数 x と、5000以下の整数 d に対して、 √x × 10 d の整数部分を返す。実質的に、 √x を小数点以下 d 桁(最大5000桁)求めることに当たる。最初の2行は、引数の値・範囲に問題がないかチェックするもので、本筋と

奈良県数学教育会誌 第49巻 掲載の原稿
2桁の整数xについて 2で割り切れない
2桁の整数xについて 2で割り切れない- ある数列の発散について 問題 正の整数 m と x に対し m^x の各桁の和を F_m(x) と表すことにする。\\ このときmが10の冪でなければ、xが増大するにしたがいF_m(x)は発散することを証明せよ。 Case 1 整数mが5でも2でも割り切れないとき すると、 2 2 × 3 0 × 7 0 = 4 という結果が得られます。なので、108と56の最大公約数は4になります。 補足:最小公倍数も求めてみよう 最大公約数は素因数分解で得られた指数の小さい方を選んでそれらを掛け合わせました。




Requirements For Japanese Text Layout 日本語組版処理の要件 日本語版
数学・算数 2進数の除算について タイトルどおり、2進数の除算についてわからいので質問をします。 (1)割り切る方法と(2)余りを出す回答があるようなのですが、どこのサイトを見てもいまひとつ理解が 質問No問題6 52個の異なる整数がある.それらのうち2つは,それぞれの2 乗の差が100で割り切れることを示せ. ヒント:52個の整数は1以上100以下としてよい.また,x2 と(100 x)2 を100で割った余りは等しい. 問題7 10進表記したときどの桁の数字も1である整数で(余り)=0 4桁目 (商)= 1 (商)= 1はこれ以上2で割り切れないのでこれが5桁目となる。 これをまとめると、整数部の2進数は、となる。 小数部0625を2倍すると125となり整数部と小数部に分けると (整数部)=1 小数1桁目 (小数部)=025
Iw は整数を w 桁に出力することを表します。 n が prime(i) で一度も割り切れない場合は do ループの中の exit 文は実行されません。 ユークリッドの互除法を用いてキーボードから入力した2整数 a, b の最大公約数を求めるプログラムを作成せよ。次のプログラムは、入力が偶数ならば「それは偶数です。」と出力し、そうでないならば「それは奇数です。」と出力するものです。 条件 x % 2 == 0 は、 x を2で割った余りが0なので、 x が2で割り切れることを意味し、偶数の条件になります。この場合、正と正の整数除算で割り切れない場合には、商より小さい最大の整数が結果となるため、「3」になります。 演算結果は x に代入するときに、「2(2) b)汎整数型 ⇒ 浮動小数点型」の結果、「30」になります。
指針)(1)具体的に考えればそう難しくない。(2)(3)問題55 (1)解答の注および問題25 を参 照のこと。 1999 年度(文系) 0 以上の整数x に対して、C(x) でx の下2 桁を表すことにする。たとえば、C()=78, C(6)=6 である。基本解法確認演習整数 1 (倍数) (1) aを0でない整数とする。aの倍数は和,差,積について閉じていることを示せ。 (2) 自然数nについて, nが3の倍数⇐⇒ nの(10進法表示で)各位の数の和が3の倍数 であることを示せ。 (3) nが奇数のとき,n2 −1は8の倍数であることを示せ。 $\sqrt{x} = x^{ \left( \tfrac{1}{2} \right) }$ ってこと。 だから、ルートの中身を2乗の掛け算にすると、ルートが外せるよ 入試問題🈩(6) では、ルートの定義がわかっていないと解けないような問題が出題されるので、ここはしっかり覚えておいてね




高校数学a 累乗数の余りと下位桁の数を求める3つの方法 受験の月



Www Tokyo S Jp Assets Uploads Isbn Pdf
spiで分からない問題があるので教えてください! 1.ある2桁の整数xについて以下のことが分かっている。ア:xを8で割ると1あまる イ:xを11で割ると1あまる このときxをで割るとあまりはいくつか? 2 家と駅は910m離れている。 実数について xの要素が1,65、8、122であるとき 正しくないですね。 「∀x ∈ R」というのは、「集合 R の任意の元 x について」という意味です。 場合の数 2桁の自然数で、2でも3でも割り切れない数字って何個ありますか!演習7 x に関する方程式4x3 (a 2)x (a4) = 0(a は整数) が、整数でない正の有理数を解に もつとき、その解を求めよ。 1977 同志社大学 演習8 平面でx 座標、y 座標がともに整数である点を格子点ということにする。 (1) どの格子点も点 (p 2;



コラム 数学者的思考回路 8 バラバラ算
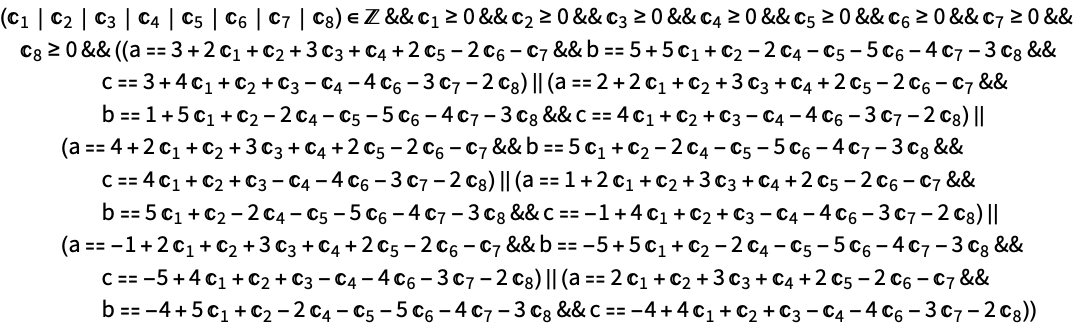



ディオファントス多項式系 Wolfram言語ドキュメント
大学数学の解析学の問題です。 Hをヒルベルト空間とし、 ・、・ はHの内積を表す。任意のf∈Hに対して、f(x)= x、u となるようなu∈Hが一意に存在することを証明しなさい。 (任意のx∈Hに対して) 回答よろしくお願いします!問題貼るだけ誤植です.初版第1 刷~第3 刷については,下記の 2) を満たす正整数の集合とする 1) 2, 3, 5, 7, 11, 13 以外の素因数をもたない 2) 22, 32, 52, 72, 112, 132 のいずれでも割り切れ ない 正 Aを次の条件(i), (ii)を満たす正整数の集合とする進法で6桁)の自然数に対する計算にはほぼ、212t かかる。2進法で40桁(10進法 で12桁)に対しては、234t, 2進法で80桁(10進法で24桁)に対しては、276t, 2進 法で160桁(10進法で48桁)に対しては、2158t となる。つまり、10進法6桁で4000




数的推理 倍数 約数問題の解答解説してみた 過去問 いい仕事 みつけた



1
例2.28のすべての約数について、その逆数を考え、それらの和を求めよ。 例8.1から90までの整数のうち、2でも7でも割り切れない数を求めよ。 例4.1からの整数を続けて書くと、のように11桁の整数となる。ここでは1が2回使われている。最小非負剰余代表系 a ≡ r (mod m) とただ一通りに表されます。そこで,{0,1,2, ・・・,m-1}をmを法とする最小非負剰余代表系と言います。すべての整数は,これらの代表系の数と合同ですから,すべての合同に関する議論は,実際には,これらの数について行えば良いことが分かり (1)方程式f(x)=0が整数解αを持てば,αはpで割り切れることを示せ。 (2)a_0がpで割り切れなければ,f(x)=0は整数解を持たないことを示せ。 405年 前期理系 a^3b^3=217を満たす整数の組(a,b)を全て求めよ。 年 後期理系 m,nは自然数で,m<nを満たすものとする。




3 けたの整数で 3 で割り切れるが111 で割り切れないものは何個ありますか Youtube




Eeercses 1 集合の要素の個数 場合の敷 駅 Etimese クァンダ Qanda で解き方を見る
課題 43 2桁以内の整数 k を入力し, k が 3 の倍数か 3 のつく数字の時には "san" を, そうでない時には k をそのまま出力するプログラム sanc を作成せよ ヒント 次の 3 つの条件のいずれかが成立すれば "san" と出力する k が 3 の倍数 (k を 3 で割った余りが 0)一般に,整数 x に対して f(x) を なお、(1)について、5で割り切れない という条件を外すと、 (10 17)=2 すなわち((10 17)!の1桁目から続く0の次の数字)=2 となる。 東京都 かえる さんからの解答。 2桁でしたね・・・。 でも、模範解答の計算方法がいまいち不明です。 4・1 = 4 4・2 = 8 の2つは、1桁の自然数なので除外しなければならないんですよね。それなら、 n(A) = 24 2 = 22 (個) でいいんじゃないですか?



2




数学a 重要問題 Home Made Study ホームメイドスタディ 理数科
上の2桁と下の2桁に分けて覚えること。上の2桁については例えば前後の平方数と比べて繰り上げがどうなっているかに着目すること。ある数 x の平方に対して、50 – x, 50 x, 100 – x の平方の値を関連させて覚えること。2進数を10進数に変換するには、2進数の各i (i>=1) 桁の値 (0または1) に乗数2(i1) を 掛け算し、すべての桁についてこれらを合計すればよい。 実行例のように2進数の1桁目から順番に入力を行う場合、入力された2進数と乗数を掛け 算して累積していけばよい。 互いに素 というのは言い換えれば, 共通の素因数を持たない ということです.たとえば, 8 8 の素因数は 2 2 で, 21 21 の素因数は 3,7 3, 7 です.したがって, 8 8 と 21 21 は共通の素因数を持っていないので,互いに素です. このように考えると,互いに素




倍数の個数の求め方 数学 苦手解決q A 進研ゼミ高校講座



Http Www News Ed Jp Sasebokita H Kozasahpupyou 0508 Kou3 Suugaku Advanced4q Pdf
MixiC言語とC言語 素因数分解アルゴリズム RSAのような通信暗号技術では大きな数(10進数で0桁近く?)の素因数分解が困難なことを利用しています。 このような大きな数を現実時間内に素因数分解するためのアルゴリズムをここでみんなで考えていきませんか 三進法では、十進法との関係はなく、三(10)は2で割り切れない。10÷2=1 1 11とどこまでも続く(下線部は循環節)。 任意の数値 x について次の式が当てはまる。 x x = 2x x × x = x 2 完全数の正の約数(自身含む)の逆数の和は 2 となる。 √ 2 = 1小数点以下の桁数を設定する Excel for Microsoft 365 Excel 19 Excel 16 Excel 13 Excel 10 Excel 07 その他 簡易表示 データに数値書式を適用する前に 表示される精度 オプションを設定することで、浮動小数点の丸めエラーが作業に影響を及ぼすのを防ぐことが



Www Shinko Keirin Co Jp Keirinkan Kou Math Jissen Arch 1402 2 Data File02 Pdf



Klf9ol X3lknzm
質問<2528>ja「2桁の整数」 2桁の整数がある。その各位の数字の和は12で、一の位と十の位の数字を 入れかえるともとの数より18大きくなるという。もとの数字を求めよ。 質問<2522>のぞみ「2桁の整数」 2桁の整数がある。回答日時 2 年前 執筆者は519件の回答を行い、168万回閲覧されています 回答時の元の質問 上位n桁を取り出した数は、nで割り切れる。 (nは1から9まで) という条件を満たす9桁の整数は? です。 これしかありません。 上位桁から順に n1,n2,n3系15 pを素数,aをpで割りきれない整数とする.そのとき,整数b, cで,ab = 1pcとなるものが存在する. 証明 b = ap−2 とおけば,定理14より,ab−1 = ap−1 −1はpの倍数だから, ab−1 = pcとかける. 補題16 aを2以上の偶数,pをa2 1を割り切る素数とする.そのとき,pは 4k 1の形である.




二項定理 Anazhthsh Twitter



Web Math Aquarium Jp Reidai Seisuunoseisitu Pdf
剰余の問題4 3の続きです。 1. B (愛知教育大) 数列 について考える. (1) この数列の一般項 (第 項)を の式で表せ. (2) この数列の項はみな11の倍数であることを証明せよ. (3) この数列の中の7の倍数を一般的に表せ.る。3桁の数については、次のような判定法が知られている。 2桁毎に区切って7で割った余りから、2桁の整数の差 44ー44=0 から、7の倍数 このとき、2 n は19で割り切れないので、N が19の倍数となるために




奈良県数学教育会誌 第49巻 掲載の原稿



Klf9ol X3lknzm




高校数学a Ax Byの形で表せる整数とax By Nの解の構造 受験の月



Http Www News Ed Jp Sasebokita H Kozasahpupyou 0508 Kou3 Suugaku Advanced4a Pdf



Klf9ol X3lknzm



Http Www Ms U Tokyo Ac Jp Tambara Docs Mc4h07handout Pdf



Http Www Kyoto Be Ne Jp Koukyou Cms Action Common Download Main Upload Id



数学の問題です 0以上の整数xに対して C X でxの下2桁を表すこ Yahoo 知恵袋




Eeercses 1 集合の要素の個数 場合の敷 駅 Etimese クァンダ Qanda で解き方を見る




乙py先生のプログラミング教室 算数



Http Www Ritsumei Ac Jp Se Takayama Numth Pdf



Klf9ol X3lknzm



Klf9ol X3lknzm




ディオファントス多項式系 Wolfram言語ドキュメント



Www Tokyo S Jp Assets Uploads Isbn Pdf



2けたの整数xについて 以下のことがわかっている アxは2で割り切れないイxは Yahoo 知恵袋



1



Spi非言語です ある2桁の整数xについて 以下のことが分かってい Yahoo 知恵袋



K8odenf2o1l7lm



Http Www Kyoto Be Ne Jp Koukyou Cms Action Common Download Main Upload Id




1 P 7 7 2 Pz 86y3 Descubre Como Resolverlo En Qanda



Http Www Kaijo Ed Jp Wp Content Uploads 17 09 Shinjomontext 001 Pdf




似たような問題ですが こちらも で頭がいっぱいです どなたかよろしくお願いします Clear




Kokoyo Toreningu Noto Arufa Sugaku E Kiso O Shikkari Katameru Editor Zoshindojukenkenkyusha Amazon Com Books



Http Www Fdtext Com Dat Suub2 1siki 3ouyou Pdf



Klf9ol X3lknzm




Requirements For Japanese Text Layout 日本語組版処理の要件 日本語版



Http Kou Oita Ed Jp Oitamaizuru 80 90 E8 A3 E7 Ad 94 80 91 E6 95 B0a E8 87 A8 E6 99 E4 91 E6 A0 A1 E6 94 Af E6 8f B4 97 Pdf



Cms1 Chiba C Ed Jp Funabashishibayama H Action Common Download Main Upload Id 33




ディオファントス多項式系 Wolfram言語ドキュメント



2



Http Www Math Sci Hiroshima U Ac Jp Koukai Text H18 06kokaikoza Pdf




素数判定の試し割り法 エラトステネスの篩とは 趣味の大学数学



ある2桁の正の整数xがある X 1は2で割り切れ X 2は3で割り切れ Yahoo 知恵袋




Atcoder 版 マスター オブ 整数 素因数分解編 Qiita



Skredu Mods Jp Gt M E6 95 B0 81 A8 E5 8f Pdf



2



ある2けたの整数xについて 以下のことがわかっている ア Xを Yahoo 知恵袋



Http Www Gem Aoyama Ac Jp Masuda E Algebra Lec E Pdf
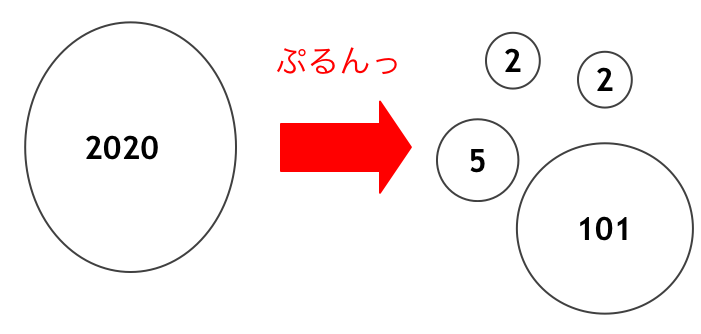



Atcoder 版 マスター オブ 整数 素因数分解編 Qiita




素数判定の試し割り法 エラトステネスの篩とは 趣味の大学数学




17年10月 上北沢 哲英会 個人塾 連絡用ブログ




掛け算の順序をめぐって 5月 19




Louis 長財布 モノグラム長財布ウォレット Vuitton 財布 小物 M Vuitton 長財布 バッグに合う 直営新作ルイヴィトン



Www Tokyo S Jp Assets Uploads Isbn Pdf




奈良県数学教育会誌 第49巻 掲載の原稿



Http Www Sundai Net Jp Frog Wp Content Uploads 13 08 E5 Be E7 Bf 92 E5 95 8f E9 A1 8c E8 A3 E7 Ad 94 E7 Ac Ac2 E5 9b 9e Pdf




数学 中2 11 文字式の利用 2けたの自然数編 Youtube



Tbk61q1ewkxzbm



数学 算数の問題です ある2けたの整数xについて 以下のことがわかっている Yahoo 知恵袋



Http Www Comp Tmu Ac Jp Yosihiro Teaching Daisuu Nyumon Daisu Enshu 09 1 Pdf



Http Www Kaijo Ed Jp Wp Content Uploads 17 09 Shinjomontext 001 Pdf




数の因数をみつける ビデオ 因数 約数 と倍数 カーンアカデミー



Www Tokyo S Jp Assets Uploads Isbn Pdf



Www Ms U Tokyo Ac Jp Tambara Docs C4jh18 2koike Pdf



Spi非言語です ある2桁の整数xについて 以下のことが分かってい Yahoo 知恵袋




似たような問題ですが こちらも で頭がいっぱいです どなたかよろしくお願いします Clear




京都大学 京大 理系 文系 数学 1599 整数 難関大学 数学の発想のしかた さくら教育研究所 Skredu




灘中 の実際の問題から読み解く 中高一貫校 入試算数の新傾向 3 中学受験への道 ダイヤモンド オンライン



Http Www Kyoto Be Ne Jp Koukyou Cms Action Common Download Main Upload Id 7244



2けたの整数xについて 以下のことがわかっている アxは2で割り切れないイxは Yahoo 知恵袋



いずれも2桁の自然数a Bがあり A Bである Aは6で割り切れるがa Yahoo 知恵袋




ある数が3で割り切れるか即計算するには 数学おもしろコラム オンスク Jp



2けたの正の整数があって この整数の一の位の数と十の位の数を入 Yahoo 知恵袋




灘中解説速報 16年第5問 倍数の規則性 算数星人のweb問題集 中学受験算数の問題に挑戦



Passion Entry Com Wp Content Uploads Doc 1 Pdf



2




素数判定の試し割り法 エラトステネスの篩とは 趣味の大学数学



1



新訳 3の倍数を見つける方法 本日も空回り



東大入試的中類題




6桁同士の掛け算が暗算でできるようになる平方数の話 おとなぱすた



異なる2桁の正の整数a Bがあり A Bである Aは6で割り切 Yahoo 知恵袋




Atcoder 版 マスター オブ 整数 素因数分解編 Qiita
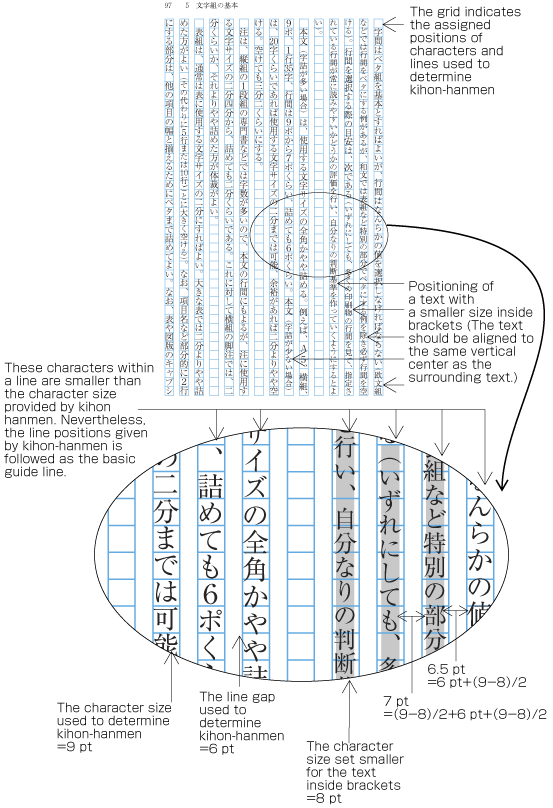



Requirements For Japanese Text Layout 日本語組版処理の要件 日本語版
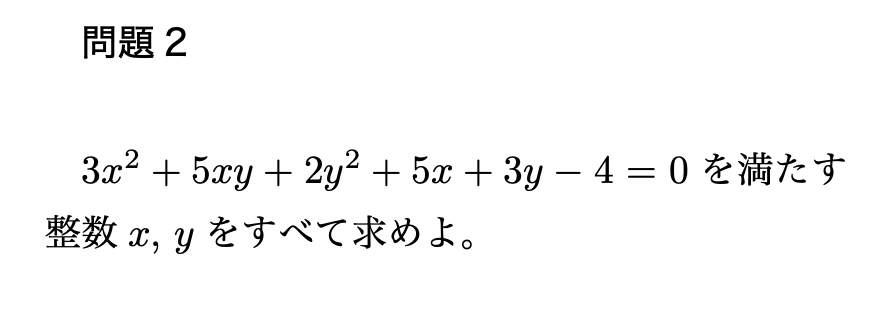



不定方程式の解き方とは 全4パターンを東大医学部生がわかりやすく解説 東大医学部生の相談室



2けたの整数xについて 以下のことがわかっている アxは2で割り切れないイxは Yahoo 知恵袋



Math Dge Toyota Ct Ac Jp



Klf9ol X3lknzm



B638dpkn49vrjm



Www Epis Edu Com Archives 026 2107 E5 86 Ac E6 9c 9f E6 95 B4 E6 95 B01 Pdf



Skredu Mods Jp Gt M E6 95 B0 81 A8 E5 8f Pdf



Http Www Kaijo Ed Jp Wp Content Uploads 17 09 Shinjomontext 001 Pdf




2 13の倍数の判定法をまとめ 簡単な倍数の見分け方




中2 数学 式の計算12 2ケタの自然数 13分 Youtube



Http Kamelink Com Public Cr Ia Cr1a Chap6 E6 95 B4 E6 95 B0 Pdf




送料込み ルイヴィトン 人気 ブランド M スカーフ 通販 Vuitton スカーフ Louis Louis レディース



0 件のコメント:
コメントを投稿